Il Percorso di Giorgio Parisi verso la Vittoria del Nobel

Il 5 Ottobre del 2021 ero a lezione di “Sperimental method for physics” quando ricevo un messaggio da un’amica: “Federica, scendi che Parisi ha vinto il Nobel!”. La lezione era ormai terminata quando leggo il messaggio e do l’annuncio alla classe con cui scendiamo a festeggiare. Tra chi va a prendere  birra, chi inizia a scrivere uno striscione e chi va a recuperare una cassa per la musica, riusciamo a mettere insieme in poco tempo dei bei festeggiamenti e Parisi esce acclamato dalla folla di studenti che cercano di allungargli il quaderno per ottenere una firma.

Nelle giornate successive sono venuti in dipartimento molti giornalisti che con fare insistente, chiedevano informazioni sul Professore, non sapendo che orma era in pensione da tempo e i suoi studenti erano già tutti laureati.

Molte narrazioni sono state fatte sulle sue ricerche e sono state avanzate spiegazioni più o meno filosofiche sul loro contenuto. Le analogie sono importanti e ci aiutano a capire  ma  è anche opportuno mettere chiarezza sul fondamento matematico delle analisi per ricordarci che la fisica che viene raccontata senza matematica non è fisica semplice ma è solo fisica semplificata.

In poche righe cercherò di darvi degli spunti sulle scoperte del Prof. Parisi che hanno gettato le basi per sviluppi nel campo della teoria dei disordini e dei sistemi complessi, trovando applicazioni pratiche in una vasta gamma di settori, dalla tecnologia dei materiali all’analisi dei dati complessi.

MODELLO DA NOBEL

Prendiamo un sistema composto da N elementi (N è una variabile, può essere 1,2,3,,,,,100000), ciascuno dei quali può assumere uno tra due stati , 0 o 1, su o giù, destra e sinistra etc…. Ogni elemento interagisce con gli altri, positivamente o negativamente a seconda che cerchi di “copiare” lo stato del secondo elemento o cerchi di fare l’opposto.

Per semplicità assumiamo che ciascun elemento possa interagire esclusivamente con i suoi primi vicini e facciamo un gioco.

Disegniamo i  siti degli elementi (1) e aggiungiamo al sistema la tipologia di interazioni che vogliamo imporci in modo completamente randomico (2). Definiamo un solo elemento di questo nostro sistema (3). A questo punto, come se fosse la settimana enigmistica, cerchiamo di completare il disegno tenendo presente che le linee dritte siano il simbolo scelto per le interazioni positive mentre quelle spezzate per quelle negative.

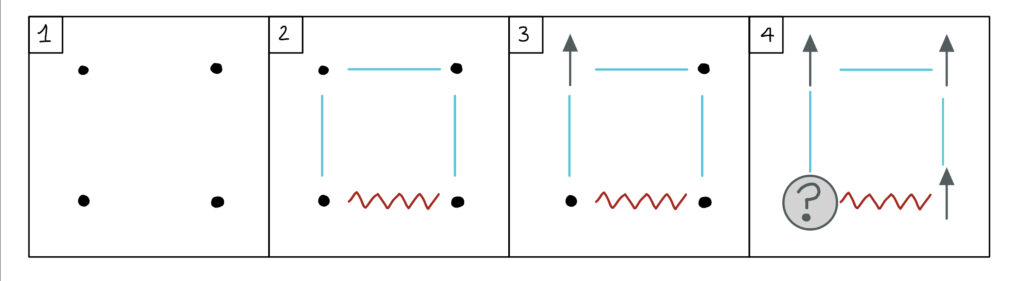
 Notate qualche problema? Il sistema è irrisolvibile. Arriviamo inevitabilmente al punto dove non possiamo conoscere a priori lo stato di un sito, questo può stare al 50 % in uno stato “sù” ed al 50 % in uno stato “giù”.

Un sistema con questa caratteristica viene definito frustrato perché può trovarsi in due configurazioni distinte con la stessa probabilità e tutti e due questi stati sono di equilibrio.

Ricordiamo che:

Un sistema tende ad andare nello stato ad energia minima che coincide nello stato di equilibrio del sistema

Nel sistema frustrato appena descritto due configurazioni sono d’equilibrio perciò ci sono due stati che minimizzano la funzione dell’energia.

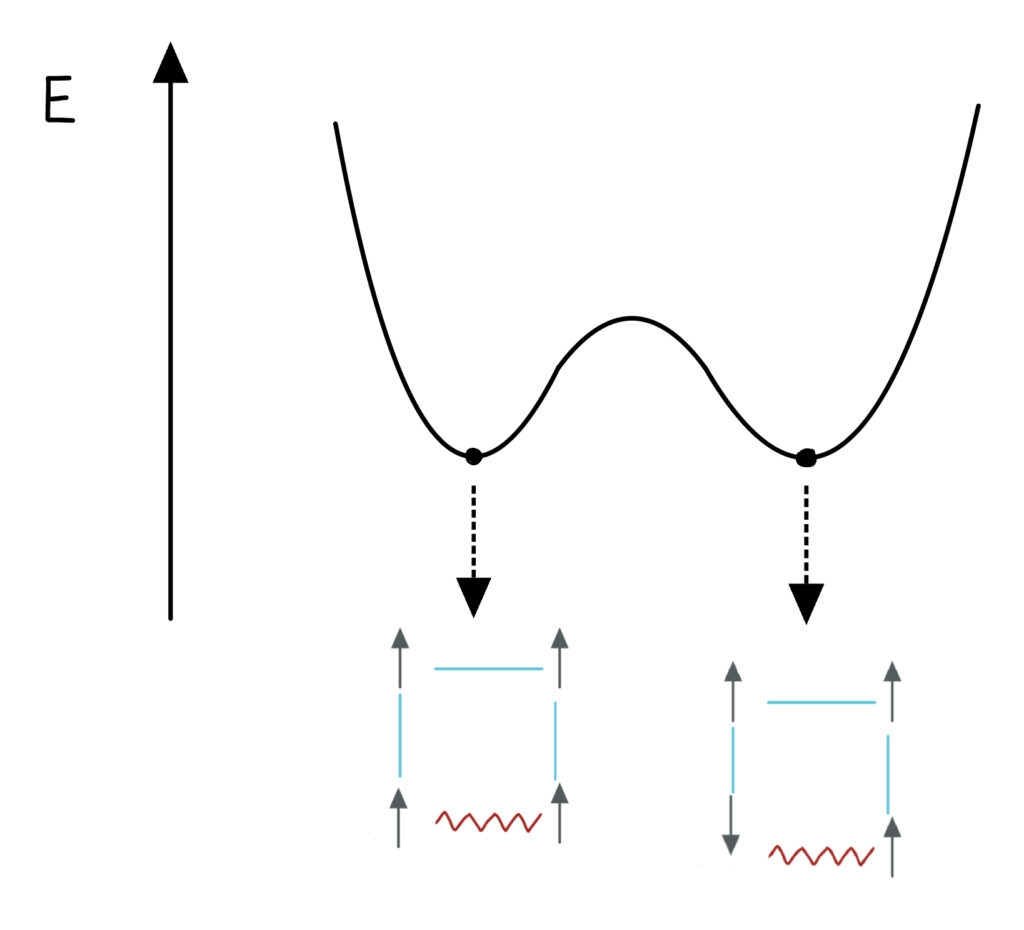
Il figura la funzione dell’energia del sistema con i due minimi corrispondenti alle due configurazioni di equilibrio

Già con 4 siti la situazione può sembrare complicata ma immaginiamoci cosa succede se aumentiamo il numero di siti a N=10^23. E complichiamo ancora le cose imponendo che ciascuno elemento possa interagire con tutti gli altri elementi (anche a distanza infinita).

 Così facendo creiamo un modello che funziona molto bene a livello teorico ma la soluzione esatta delle equazioni che lo descrivono è difficile da trovare, dato che il numero di minimi (e quindi di stati di equilibrio del sistema) diventa estremamente grande.

Per risolvere questo problema il Prof. Giorgio Parisi ha sfruttato il cosiddetto “trucco della replica”. Si tratta di un trucco matematico in cui per studiare un sistema disordinato ed imprevedibile, lo si riproduce più volte creando copie distinte ed indipendenti multipli del sistema originale. Attraverso l’uso di calcoli matematici e tecniche di media su queste repliche , è possibile far emergere degli schemi rivelatori del quadro originale.

TRUCCO DELLA REPLICA

  Un lettore estremamente attento può cogliere una falla in questo metodo… l’obiettivo era quello di studiare un sistema singolo, ma se lo riproduco più volte sto ovviamente studiando più sistemi insieme e non era l’obiettivo che si voleva raggiungere. Eppure si dimostra che nelle equazioni finali del calcolo non è troppo complicato ricondursi ad un singolo sistema, questo risulta discretamente facile.

Riassumendo il trucco della replica

1. Prendo un sistema disordinato e frustrato si cui non riesco a trovare la soluzione esatta
2. Moltiplico questo sistema M
3. Cerco dei pattern generali degli M sistemi individuando dei comportamenti comuni
4. Riporto M a 1

In realtà Parisi non fu il primo ad impostare il problema in questo modo. Già Edwards e Anderson lo avevano fatto nel 1975, ma nessuno aveva molta fiducia in questo trucco per due ragioni fondamentali. Prima di tutto perché non c’era molto fondamento matematico che tutto questo stesse in piedi e secondo poi perché le analisi dei due scienziati cadevano in conclusioni assurde che nessun fisico sarebbe mai stato disposto ad accettare.

Quando Parisi inizia a studiare gli articoli e Edwards e Anderson inizialmente ipotizzava un errore nei calcoli. Non trovandolo, ricerca in queste ricerche un punto di vista innovativo.  Capisce che replicare un sistema M volte non voleva dire replicarlo perfettamente ma voleva dire replicare il suo stato di equilibrio. Come abbiamo visto dalle considerazioni precedenti questi sistemi hanno molti stati di equilibrio perciò replicare M volte vuol dire avere M sistemi ciascuno dei quali in uno stato di equilibrio. Ma come abbiamo visto, per questi sistemi abbiamo diversi stati di equilibrio e non è detto che le repliche siano tutte nello stato d’equilibrio del sistema originale. Così facendo la ricerca di Giorgio Parisi ha chiarito cosa succede quando la frustrazione si manifesta in sistemi disordinati e complessi. Con il suo lavoro , ci ha permesso di trarre conclusioni senza precedenti su questi sistemi, che solo apparentemente sembrano casuali ed imprevedibili.

DAL MODELLO ALLA PRATICA

Il modello descritto nel capitolo precedente è stato studiato da Parisi per descrivere i “vetri di spin”*. Ma le potenzialità del modello sono infinite. E’ stato per esempio usato per capire la struttura delle proteine ed il perché, nonostante esistimo milioni di combinazioni possibili di struttura delle proteine (partendo da soli 20 amminoacidi) si verificano sono un centinaio di queste strutture proteiche. Il modello è anche stato sfruttato nel campo del Machine learning e delle reti convoluzionali.

L’intuizione e genialità del fisico sono state anche ampliamente sfruttate nel ambito climatico. Nei primi anni ’80 lo scienziato ha iniziato a studiare contributo delle dinamiche interne degli oceani e dell’atmosfera (schematizzati come rumore) sommato al contributo delle variazioni del flusso di energia del sole e come questi contributi si sommino per studiare le variazioni di temperatura terrestre. Non a caso il professore divide il premio nobel con i  climatologi Syukuro Manabe e Klaus Hasselmann che hanno gettato le basi delle nostre conoscenze del clima della Terra e di come le attività umane lo influenzano.

*magnete che può mostrare in modo casuale proprietà sia ferromagnetiche che antiferromagnetiche a causa della distribuzione probabilistica degli elementi interni che producono gli effetti magnetici.

Il RUOLO POLITICO DEL PROF. PARISI

Mi preme sottolineare l’età dei ricercatori che hanno partecipato alla ricerca climatica affiancando il Professore.

Parisi (1948) aveva 32 anni ed era il più anziano di quel gruppo (il più giovane aveva 22 anni). Oggigiorno uno scenario del genere sembra quasi impossibile a causa dei tempi della ricerca accademica ed a causa della carenza dei fondi nella ricerca in italia. Oltre al suo percorso accademico eccellente, Parisi ha sempre dimostrato una grande sensibilità nel settore politico della ricerca, esprimendo dissenso per i pochi fondi dati alla ricerca in Italia soprattutto nell’ambito dei sistemi complessi.

Parisi è motore della campagna #salviamolaricerca che nel 2016 chiese all’unione europea di fare pressione sul governo italiano  perché finanzi adeguatamente la ricerca portando i fondi a un livello superiore (3%), richiamandolo a fare il proprio dovere in questo settore cruciale per il futuro del paese.

I dati sui finanziamenti in ricerca e sviluppo in percentuale sul PIL collocano l’Italia agli ultimi posti. Il Sistema Universitario Italiano è da anni sottofinanziato (il fondo di finanziamento ordinario alle università è in continua discesa dal 2009 ad oggi). I fondi per la ricerca di base italiana, distribuiti su base competitiva ai progetti scientifici che sono valutati più validi, sono dieci volte di meno di quelli della Francia.

Nonostante questo la qualità della ricerca italiana è attestata da più di un indicatore: l’Italia l’ottava nazione al mondo per articoli scientifici pubblicati, mentre è la settima per il loro impatto.

Federica De Riggi

Laureata in fisica a Roma mi sono specializzata in fisica delle particelle ad alte energie, collaborando con gli esperimenti di LHC. Mi diletto in arti figurative e grafiche e mi diverto sfruttando questa passione per sintetizzare concetti che si astraggono dietro delle formule. Nel mio percorso ho capito che nulla è difficile una volta compreso. Le giuste parole sbloccano un percorso nella mente di chi ascolta e solo percorrendo quel percorso un concetto resterà impigliato addosso. Da qui il potere delle parole.