La luce va dritta sulla strada dello spaziotempo

La teoria della Relatività Generale, maestosa opera di Albert Einstein, fu pubblicata nel 1916. Tale teoria ha rivoluzionato la nostra concezione dello spazio e del tempo, mostrandoci come queste due quantità siano i fili di un tessuto presente nell’universo sul quale i pianeti e le galassie si appoggiano, deformandone la trama e l’ordito. In questo scenario, che ha rivoluzionato la nostra visione dell’universo, permettendoci di costruire tecnologie mai pensate e possibili prima, tutto si muove seguendo la forma di tale struttura, anche la luce.

Immaginiamo un raggio luminoso che si muove in linea retta: Newton ci insegna, nei suoi principi, che per perturbare lo stato di moto rettilineo di un corpo è necessario che su di esso agisca una forza F e, negli stessi principi, afferma come tale forza sia proporzionale alla massa m e alla accelerazione del corpo a, secondo la celebre formula:
F=ma
Ma la luce, essendo priva di massa e muovendosi a una velocità che non può aumentare, è possibile che curvi? La risposta data dalla Relatività Generale è affermativa ma non per motivi spiegabili con il lavoro di Newton.
Vediamo ancora un attimo come la equazione di Newton perda il suo significato per questa quantità senza massa, ripercorrendo alcune delle più importanti scoperte del XX secolo.

Nel 1905 Einstein pubblicò il suo lavoro sulla Relatività Ristretta. Uno dei risultati più sorprendenti di questo lavoro è condensato nella seguente formula:
E=mc²
Questa formula mi dice a quanto equivale la energia E di un corpo di massa relativistica m; massa relativistica significa che se il corpo è fermo, tale valore corrisponde con la usuale concezione di massa che abbiamo tutti, quella che si può pesare con una bilancia, mentre se il corpo si sta muovendo, tale valore diventa più grande di quella solita perché il nostro movimento ne aumenta la energia. Il punto di tale formula è quello di affermare come l’energia E e la massa m siano in proporzione diretta. I fisici teorici spesso danno a c, essendo costante, il valore 1 così che nei loro fogli abbiano
E=m
una formula molto semplice e comoda da usare che mi dice: dove c’è massa c’è energia.
Qualche anno prima, nel 1900, il grande fisico tedesco Max Planck, aveva già rivoluzionato la fisica con un’altra formula:
E=hv
Questa formula stabilisce la energia E di un fotone, la particella che costituisce la radiazione elettromagnetica e che si muove alla velocità della luce; in tale equazione compare h, la costante di Planck che vale 6,626075⋅10^-34 J⋅s, e v ovvero la frequenza della radiazione che indica la rapidità delle oscillazioni dell’onda. Siccome ai fisici piace semplificarsi le equazioni, e quindi la vita, spesso pongono il valore della costante h pari a 1, così da avere:
E=v
Anche qui, dove c’è qualcosa che oscilla c’è energia. Cosa succede se prendo i due risultati semplificati e li unisco?
m=v
Lì dove c’è una massa c’è anche una frequenza…quindi? Beh, la frequenza è quella quantità che ci permette di tenere il conto del tempo, ogni orologio segue un battito che, ripetendosi, ci permette di scandire lo scorrere dei secondi. Quindi lì dove c’è una massa c’è la possibilità di contare il tempo. Tutte queste considerazioni sono valide per noi essere umani, abbiamo una massa e contiamo il tempo. Ma se la massa, come nel caso della luce, è pari a zero?
Ecco, per un fotone, di massa zero, non esiste lo scorrere del tempo, lui non invecchia, è un eterno giovane, anche se questa parola perde di significato non esistendo per lui il concetto di vecchio, è semplicemente eternamente sé stesso.
Se per curvare, quindi, è necessaria una forza esterna che Newton dice essere legata alla massa e alla accelerazione, come fa la luce a percorre delle strade curve nel suo propagarsi nello spazio, tra i pianeti, se non ha massa e non conta il tempo?
Senza entrare nei dettagli matematici la questione può essere riassunta così: se nella nostra esperienza lo spazio è percepito come piatto e per curvare deve agire una forza esterna a perturbare il nostro movimento rettilineo, per la luce avviene il contrario: le sue traiettorie sono sempre rettilinee ma lo spaziotempo curva per lei. Quindi nelle equazioni che descrivono le orbite della luce devono entrare in gioco le informazioni su come sia composto lo spaziotempo, cosa assente nella equazione di Newton F=ma, dove non c’è scritto in che tipo di spaziotempo mi trovo.
La questione da mettere a fuoco è che per noi, oggetti macroscopici, c’è la possibilità di scegliere quando curvare perché nella equazione non ci sono informazioni riguardo allo spaziotempo, mentre per la luce è lo spaziotempo a decidere quando deve girare….in fondo siamo fortunati nel poter scegliere.

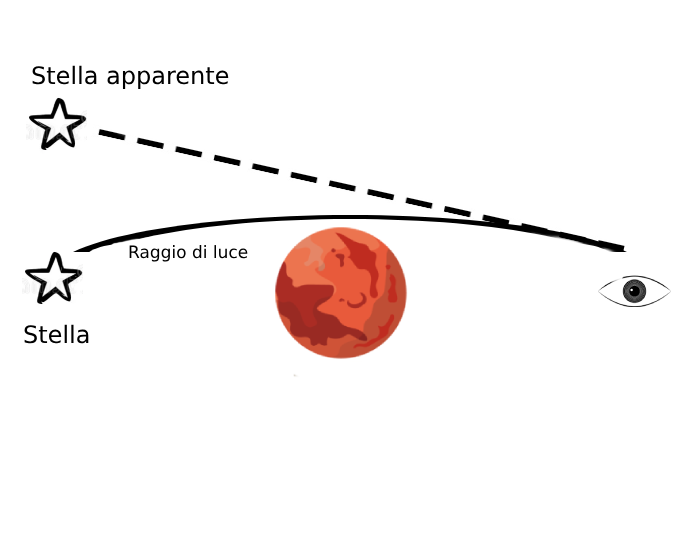
Verifiche sperimentali

Il fenomeno della curvatura della luce è stato verificato sperimentalmente e rientra tra le prime tre verifiche che hanno portato alla affermazione della teoria della Relatività Generale. L’effetto più caratteristico di questo fenomeno è dato dalla possibilità di poter osservare, dalla Terra, delle stelle che si trovano dietro a pianeti che ne occultano la vista; dalla immagine successiva possiamo vedere come la luce di una stella posta dietro al pianeta compia un percorso curvo, superando il pianeta stesso arrivando al nostro occhio o al nostro telescopio. Bisogna ricordarsi, però, che il nostro cervello vedrà la stella in una posizione diversa da quella vera, come quando immergiamo una cannuccia in un bicchiere pieno d’acqua

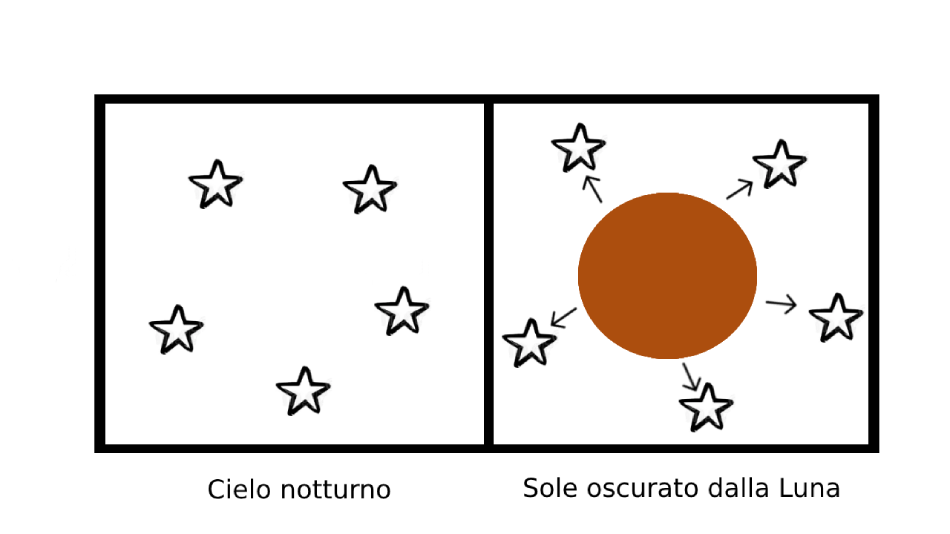
La prima spedizione che si occupò della verifica di tale fatto risale al 1919 e fu portata avanti dal direttore dell’osservatorio di Cambridge Sir Arthur Eddington che raggiunse l’isola del Principe al largo della costa occidentale dell’Africa; l’astrofisico era interessato a misurare la posizione delle stelle in presenza e in assenza del Sole per poi compararne lo scostamento e verificare o meno la teoria di Einstein.

Come fecero a misurare la posizione delle stelle di giorno? Si sfruttò la presenza di una eclissi totale di Sole che oscurò completamente la sua luce e permise di effettuare le fotografie necessarie; le lastre fotografiche ottenute in questo preziosissimo momento vennero comparate con le fotografie scattate al cielo notturno, e questo confronto diede testimonianza di una deflessione della luce in totale accordo con la nuova teoria.

Non fu facile ottenere tali risultati a causa di problemi legati alla emulsione fotografica ed errori sistematici che dettarono la necessità di operare numerose misurazioni diverse, problematiche oggi largamente superate dai nuovi radio telescopi e dalle osservazioni dei quasar, delle sorgenti luminose quasi puntiformi che emettono un enorme quantitativo di radiazione elettromagnetica.
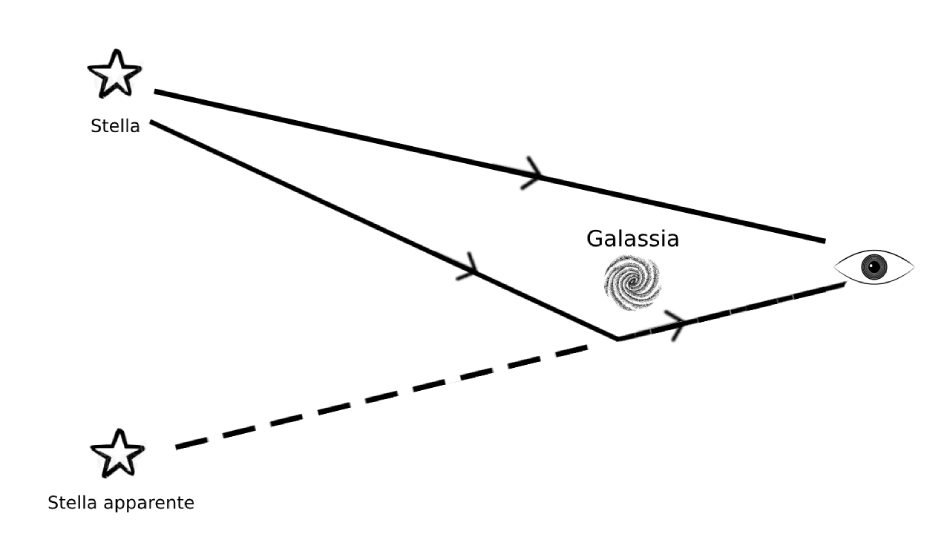
Questo strano effetto può portare anche ad altre vere e proprie illusioni; un oggetto molto lontano nello spazio può creare una doppia immagine al nostro occhio.
Se consideriamo infatti il seguente disegno, vediamo che la traiettoria della luce, percorrendo due strade diverse, arriverà ai nostri occhi da due diverse direzioni, illudendoci che l’oggetto che emana luce si trovi contemporaneamente in due posizioni diverse.

Furono proprio degli astri a portare il nome di Einstein a essere scritto tra le stelle del firmamento scientifico. Le implicazioni della sua teoria sono numerosissime, ancora oggi avvolte da mistero.
Prossimamente il nostro raggio di luce ci porterà nelle vicinanze di un buco nero: cosa succede in questi luoghi estremi e fondamentali per studiare la fisica contemporanea? La questione è ancora aperta.

Antonio Sandroni

Sono Antonio Sandroni, laureato in Fisica Teorica all’università di Bologna. Attualmente lavoro in una società di Marketing e comunicazione ma la mia vera occupazione è camminare sui ponti che collegano il sapere tecnico-scientifico a quello umanistico, esplorando l’universo tramite la fisica, la poesia e la letteratura, le quali sono vele dello stesso vascello che naviga l’Universo. “Non entri qui chi non è geometra” diceva Platone, perché tutto il sapere è volto a conoscere la geometria e la direzione del cosmo.